This is a follow-up article on Machine Learning, Part 2. Have you read the introduction to Machine Learning (Part 1) already?
The next thing I wanted to learn in my journey was to make a neural network recognize the digits in this picture. It’s a very well-known problem, and there’s countless articles written about it (and this particular set of digits), but that’s what makes it a good first problem to tackle, and a good way to learn neural networks. So how do we get there? How do we make a computer see the numbers, and what even is a neural network anyway?

The next thing I wanted to learn in my journey was to make a neural network recognize the digits in this picture. It’s a very well-known problem, and there’s countless articles written about it (and this particular set of digits), but that’s what makes it a good first problem to tackle, and a good way to learn neural networks. So how do we get there? How do we make a computer see the numbers, and what even is a neural network anyway?
What is a neural network?
At work every day, for our clients, we program algorithms. This is a term with an incredibly loaded history and whose definition is hard to really pinpoint, but in this context I’m going to define it as a computer program. Something that receives a context or input, follows a pre-programmed set of rules and procedures, and arrives at a result or output.
Where a machine learning algorithm differs, is that instead of having prewritten rules, it only has a bunch of knobs called parameters, which are initially set to random values. And it tweaks them continuously — every time you show it an example until the output is what we want given a certain input. The more data you have, the more those parameters will be tweaked in meaningful ways.
This is the same way we operate: if this is the first time you’re seeing a dog in your life you’re just going to think “A dog is something with four legs” but if I show you tons of animals, including different breeds of dogs, you’re going to more meaningfully pinpoint what makes a dog a dog.
Originally most machine learning algorithms and techniques come from statistics and probabilities and weren’t actually invented to replicate intelligence in meaningful ways. Techniques like Naive Bayes or Decision Trees are at their core purely logical and mathematical and just so happen to fit this paradigm of “learning through data.” As such, they were the early successes of machine learning and, for a long while, this form of classical machine learning was all there was to it.
Now, in contrast to that, neural networks started as a purely theoretical representation of how our brains and intelligence work, and they date back to the 19th century. In fact, it was only in 1943 that the first computer neural network was made, and it took decades of trial and error, improvements, and failures for them to become as powerful and versatile as they are nowadays. But at their core they are just one of the many many available machine learning algorithms. They just so happen to be the ones with the most success in recent years and the ones that most closely resemble how our own intelligence works.
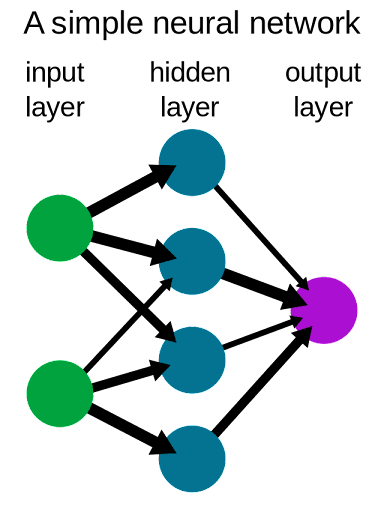
I’m not going to dive too much into the inner workings of neural networks because it’s a very complex topic, but the gist is that they’re made of a succession of many layers, each composed of many artificial neurons. Data flows from the first layer (the input layer), through every single neuron, until it reaches the last layer (the output layer).
The layers in between the input and output, called the hidden layers, come in many different shapes and types depending on the problem you’re trying to solve. Some types of layers are better at images, some are there purely to transform the data, some are there to prevent your network from just memorizing stuff, and so on. When people talk about deep learning, they mean machine learning through deep neural networks: networks with a lot of layers.
Wide neural networks, that have very few layers but many many neurons per layer, are in contrast with deep networks. We mostly use deep networks these days because they perform much better than wide networks while still being able to reach the same capabilities.
But a single layer network, if that layer was wide enough, could solve any problem you throw at it, just very, very slowly because it would need to hold and consider a dramatic amount of information in memory at once whereas a multilayered network can consider things in smaller increments.
Each neuron in a layer has its own set of parameters (called its weights and biases) that tells it when to “light up” or not depending on if its neighbors are also lit up, which allows it to react to different stimuli in meaningful ways much like biological neurons would. So what does that mean in practice? How does that allow a neural network to see digits?
Computer vision
If we take a single drawn digit, it’s first going to be transformed in a way that a computer can understand. That means it’s going to be turned into pixels, each one being a single grayscale value representing how much “number” that particular pixel is showing. A pixel value of 0 means there is no number, a pixel value of 255 means there is hella number.
In the case of the MNIST dataset I’m using (called so because it was originally made by NIST), images are 28×28 which means each digit is fed into the network as 784 integers. Those are fed straight up to the input layer which accordingly will have 784 neurons. Neurons that light up will be the ones seeing parts of the digit while the ones staying off will be the ones seeing the empty space in the image.

Once our network has received the image through its input layer, it needs to Do Stuff™ to it. Think about what your brain does when you see a digit, how do you differentiate whether you’re seeing an eight in the image above or a six?
You’re first going to look for small details (curves, lines), then your brain is going to build up those small details into larger details (the loops and holes), and finally it’s going to assemble those larger chunks into the number itself. You don’t immediately see the eight (even if it feels like it), but you see an arrangement of a multitude of small details which, when lined up a certain way, has been associated with that number in your mind’s pattern matcher.



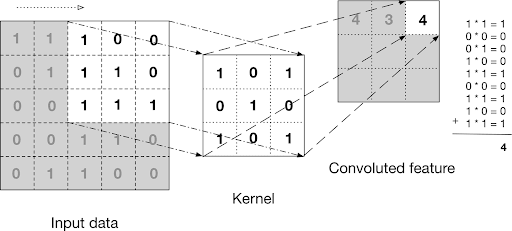
Neural networks work exactly the same way. Once the data is inside our input layer, it’s going to be passed through several convolutional layers — a popular kind of layer. It’s hard to explain extensively what a convolution is in simple terms, but in this particular case they essentially do the same thing your brain does. They make each neuron look at a small bunch of neighbor pixels at a time, summarize them a certain way (depending on what that neuron is looking for — this is called a kernel), and pass down that summary to the next layer.
The way each neuron summarizes what it sees is unique to it and is not something that is programmed. As the neural network learns to tweak its parameters to reach a given output, the neurons will gradually learn to extract relevant features off the image themselves, simply through positive feedback loops.
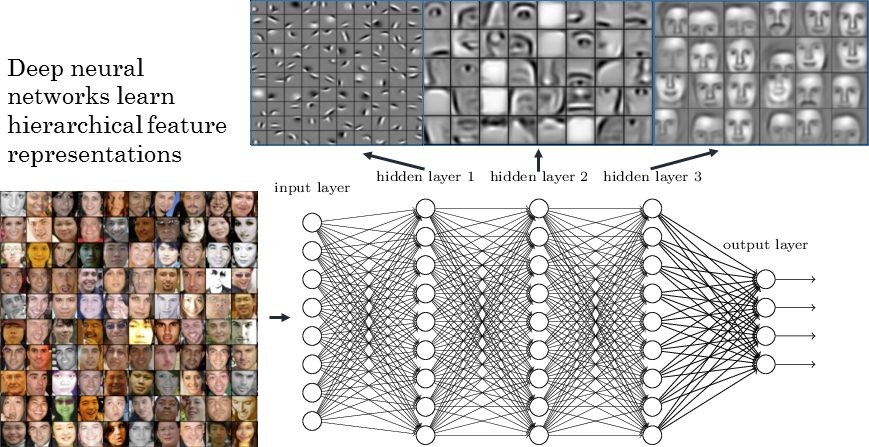
Some neurons in the early layers will learn to recognize straight lines or curves, while layers down the line will build upon those and learn to see loops or tails. This process is identical no matter what the network is trying to see, be it digits, faces, or even spectrograms and charts. All it sees are pixels, and how those pixels relate and build up upon one another.
Here is a very simplified example of what this process looks like for faces: see how it starts by recognizing very simple and abstract features such as edges and reliefs, and gradually assembles those until you have neurons that activate upon seeing certain kinds of faces.
Once you’ve trained all your convolutional layers, you give it a good shake and pour the resulting neuron activations into your output layer which represents what we’re trying to predict. Here we have 10 numbers we can predict (0 to 9) so we’d have a layer of 10 neurons. If the second to last output neuron lights up when it sees our image, then the network thinks it’s seeing a 8. Tada!
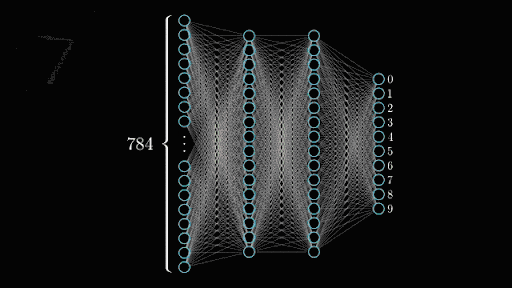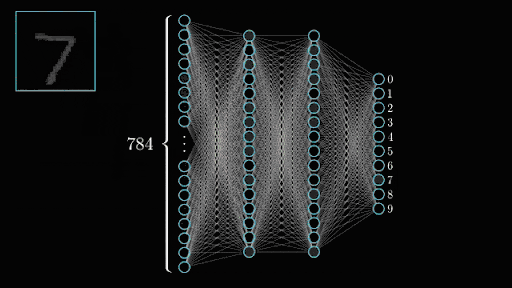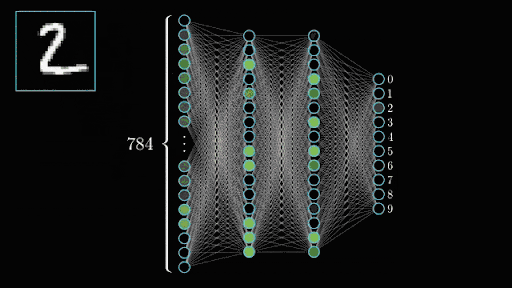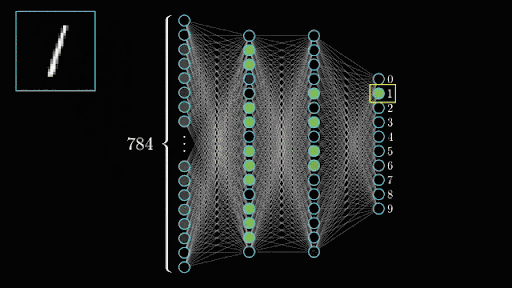
Neural training
So this is the theory of it, but there are, of course, myriad subtleties to this. You can’t just sandwich two or three convolutional layers between your input and output and get perfect digit recognition. What differentiates a good network from a bad one is not (just) the data you feed into it, but the way you arrange the layers and which kind of layers you arrange. This is called the network’s architecture, its blueprint if you want. There are some principles and general knowledge you can apply to figure out the perfect architecture for your problem, but at the end of the day the best way is through experiments and trial and error.
To measure how well an experiment worked, we use cross-validation. Which means keeping some of the training data hidden from the model until we want to verify how well it actually does. Imagine we have 10 digits. You’d train your model on 7 random ones and when you’re done, you show it the 3 you left out.
If the model doesn’t label those correctly, then that means it just memorized the first 7 very well and didn’t actually learn to recognize random digits but just the first set. The goal is to set up a poor version of your model very early where you measure accuracy. Then, every single change you make to the architecture can be scored. This is called a baseline model and is one of the most essential steps in training a model.
I personally used Weights and Biases for this, which is a service that allows you to add a callback to your model and have every experiment tracked and analyzed. It allows you to see the code of every run, draw graphs, create reports, etc. It’s a pretty amazing tool and I don’t really see myself doing machine learning without it, to be honest.
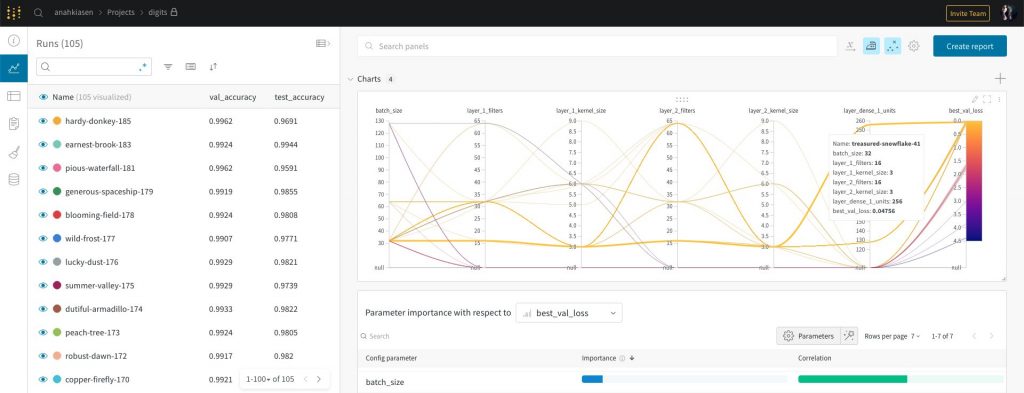
Once you have your baseline, the second step is to overfit it, meaning make it score as high as you can on the training data. Throw a lot of firepower at the problem; make a network so complex it can memorize every single digit you show it if need be. If you can’t make your model learn by heart, it means it’s likely too dumb to learn at all.
Only once you’ve reached very high training accuracy, you should start adding layers that make the model good at generalization. For example, you can add dropout layers which straight up drop random chunks of the data before passing it to the next layer, to prevent the network from memorizing too much.
Another tool that greatly helped me reach this level of accuracy is called data augmentation, which is when you apply random transformations to your data to make your network more robust. For example, in our case, all the digits are mostly straight and clean, so we apply data augmentation to them like rotating some of them by 45° and such so that the network is able to recognize a six even if it is slanted or deformed.
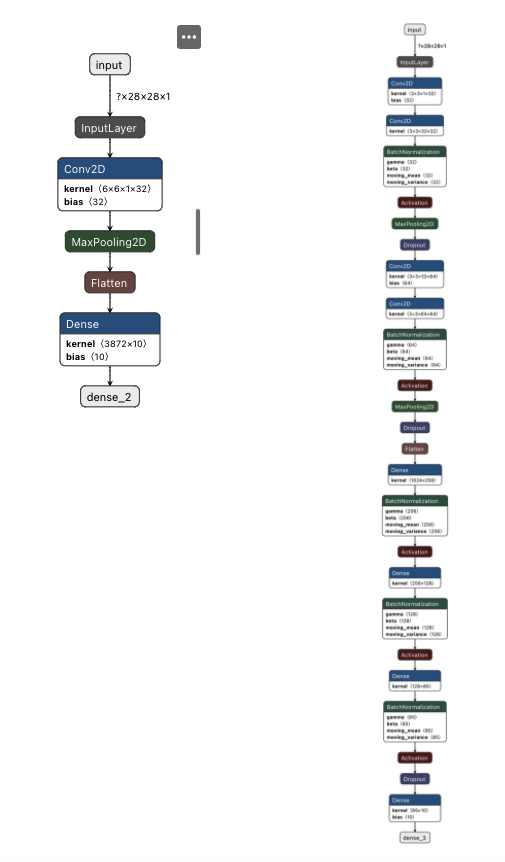
It took me 105 experiments to make a model that reaches 99% accuracy. I learned an amazing amount of things about neural architectures all throughout: what kind of layers you use, how to tweak them, and the importance of each parameter of those layers. Here are side-by-side comparisons of the architecture I started with for my baseline and the one I ended with. (It is not the only architecture that does well at this problem, just the one I ended up with organically. There are many more performant and leaner ways to tackle this problem than my naive result.)
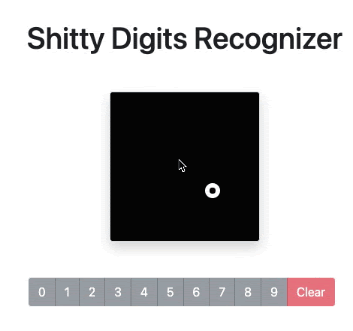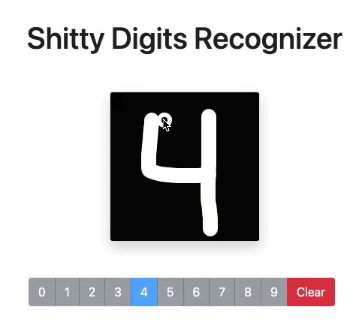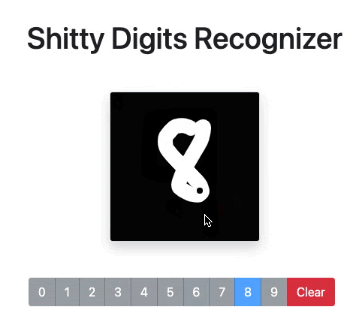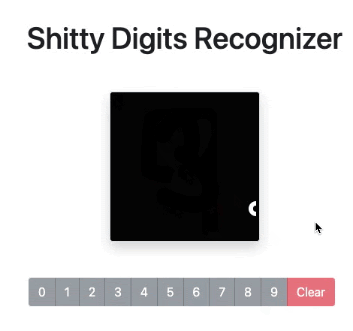
Because I wanted the full experience, I’ve deployed my model to production into a very barebones application that you can find here. Bear in mind that it reached 99% accuracy at this particular dataset and that you’re likely going to draw shapes of digits that it never saw before and will fail to recognize. So take that number with a huge grain of salt.
As a bonus you can watch here the first convolutional network demonstrating its efficiency at this very task in 1993.
Next steps
Now that I’m done with digit recognition and that I’m much more familiar with neural networks, I can move on to the topic that gives me passion: generative networks (models that create stuff).
So my next mission will be another very well known problem: the MonetGAN competition. It involves training a model that can turn normal photos into paintings of famous painters and vice versa. If you’ve used some of the “Toonify me” apps that have been doing the rounds, those are the same kind of neural networks.

I’m also interested in something that is very important in machine learning. Models inherit the biases of everything that led to them being put into production. And countering those biases — in the data, in the validation process, in the ways the model will be used in real life — is the current gordian knot that the field of AI ethics is trying to tackle.
See you next time!









Member discussion